Gravitation is the force responsible for the attraction between objects with mass. It’s responsible for the motion of celestial bodies and objects falling towards the Earth. Sir Isaac Newton established the concept of the gravitational force.
Centripetal Force:
Spiraling Secrets: Revealing the Centripetal Force Mystery
Gravity: Earth, Apple, and Newton’s Laws in Motion
Planetary Orbits and the Cosmic Dance of Celestial Bodies
Universal Force: Bridging Celestial Force
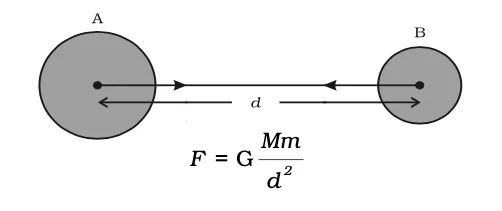
F∝ M × m
F∝ 1 / d2
Combining both we get:
F ∝ M × m / d2 or F = G (M × m / d2 ),
where G is the Universal Gravitational Constant.
F × d2 = G M × m or,
G= F × d2 / M × m
|
Example: The mass of the earth is 6 × 1024 kg and that of the moon is 7.4 × 1022 kg. If the distance between the earth and the moon is 3.84 × 105 km, calculate the force exerted by the earth on the moon. (Take G = 6.7 × 10–11 N m2 kg-2) Solution: The mass of the earth, M=6 × 1024 kg The mass of the moon, m=7.4×1022 kg d = 3.84×105km = 3.84×105×1000m = 3.84 × 108 m G= 6.7×10–11 N m2 kg–2 The force exerted by the earth on the moon is F = G (M × m / d2) = 6.7×10−11 N m2 kg-2 × 6 × 1024 kg × 7.4 × 1022 kg / (3.84 × 108 m)2 = 2.02 × 1020 N. |
|---|
<div class="new-fform">
</div>
