Newton’s Laws and Celestial Forces

Gravitation is the force responsible for the attraction between objects with mass. It’s responsible for the motion of celestial bodies and objects falling towards the Earth. Sir Isaac Newton established the concept of the gravitational force.

Moon’s Motion: The Dance of Gravitational Forces

• Revolution: The moon revolves around the earth.
• Newton’s View: Newton postulated that the same force that causes an apple to fall to the ground also keeps the moon in its orbit around the Earth.
• Orbiting Earth: Although the moon seems to orbit the Earth without falling towards it, that is where the concept of centripetal force comes into play.

Centripetal Force: 

• When an object moves in a circular path, the force that keeps it moving along that path and prevents it from flying off in a straight line is called the centripetal force. 
• Without this force, an object in motion would continue in a straight line, tangent to the circular path.

Spiraling Secrets: Revealing the Centripetal Force Mystery

• The moon’s orbit around the earth can be attributed to centripetal force. 
• This force is a result of the gravitational attraction between the Earth and the moon. 
• Without this gravitational force, the moon would not revolve around the Earth but would move in a straight line.

Gravity: Earth, Apple, and Newton’s Laws in Motion

• While it is evident that the earth attracts objects, like an apple falling from a tree, the opposite is also true. 
• According to Newton’s third law, the apple exerts an equal and opposite gravitational force on the earth.
• However, due to the enormous mass difference between the earth and an apple, the resulting acceleration of the earth towards the apple is minuscule and imperceptible.

Planetary Orbits and the Cosmic Dance of Celestial Bodies

• Planets in our solar system revolve around the Sun due to the gravitational pull the Sun exerts on them. 
• Newton deduced from these observations that all objects in the universe exert gravitational forces on each other, irrespective of their size.

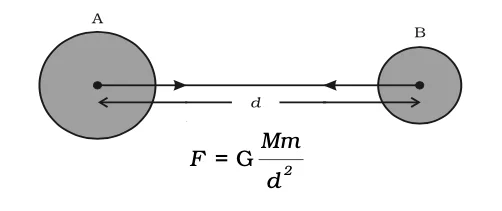
Universal Force: Bridging Celestial Force

• Gravitation is a universal force that attracts objects with mass towards each other. 
• This force is crucial for the functioning of our universe, governing the movement of celestial bodies and determining how objects behave on the Earth.

Unlocking the Mysteries of Gravitation: The Universal Law Revealed

• Understanding Concept: Every object in the universe attracts every other object with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centres.
• Mathematical Representation: For two objects A and B of masses M and m respectively, separated by a distance d: 

F∝ M × m 

F∝ 1 / d2

Combining both we get: 

F ∝ M × m / d2  or F = G (M × m / d2 ), 

where G is the Universal Gravitational Constant.

• Value of G: The constant G, called the universal gravitational constant, has an accepted value of: 

F × d2 = G M × m or,

G= F × d2 / M × m

• This value was determined by Henry Cavendish using a sensitive balance.
• Perceptibility: While this law means there’s a gravitational force between any two objects (like you and your friend), it’s usually much too weak to be noticeable unless at least one of the objects has a very large mass, like a planet.
• Universality: The law is applicable universally, irrespective of the nature, size, or location of the bodies. 
  • For instance, if the distance between two objects is doubled (increases by a factor of 2), the gravitational force between them becomes a fourth (1/4) of its original value.

DOWNLOAD PDF