How does the Spherical Lens Shape Impact Light Refraction?

• Spherical lenses: Curvature of Optical Precision: A transparent material bound by two surfaces, of which one or both surfaces are spherical, forms a lens. 
  • This means that a lens is bound by at least one spherical surface. 
  • In such lenses, the other surface would be plane. 
• Double Convex Lens: Optical Prowess through Dual Spherical Surfaces: A lens may have two spherical surfaces, bulging outwards. 
  • Such a lens is called a double convex lens. 
  • It is simply called a convex lens. 
  • It is thicker at the middle as compared to the edges. 
• Converging Lenses: Optical Power in Convex Marvels: Convex lenses converge light rays. 
  • Hence convex lenses are also called converging lenses. 
• Diverging Lenses: Optical Expansion through Concave Marvels: A double concave lens is bounded by two spherical surfaces, curved inwards. It is thicker at the edges than at the middle. 
  • Such lenses diverge light rays. 
  • Such lenses are also called diverging lenses. 
  • A double concave lens is simply called a concave lens. 
• A lens, either a convex lens or a concave lens, has two spherical surfaces. 
  • Each of these surfaces forms a part of a sphere.
• Centre of Curvature  in Lenses: Focal Heart of Optical Precision: The centres of these spheres are called centres of curvature of the lens. 
  • The centre of curvature of a lens is usually represented by the letter C. 
  • Since there are two centres of curvature, we may represent them as C1 and C2. 
• Principal Axis in Lenses: Mapping the Optical Axis of Precision: An imaginary straight line passing through the two centres of curvature of a lens is called its principal axis. 
  • The central point of a lens is its optical centre.
  •  It is usually represented by the letter O. 
  • A ray of light through the optical centre of a lens passes without suffering any deviation. 
• Aperture in Spherical Lens: The effective diameter of the circular outline of a spherical lens is called its aperture.
• Principal Focus on Concave Lens: Convergence of Light Rays: Several rays of light parallel to the principal axis are falling on a convex lens. 
  • These rays, after refraction from the lens, are converging to a point on the principal axis. 
  • This point on the principal axis is called the principal focus of the lens. 
• Principal Focus on Concave Lens: Divergence of Light Rays: Several rays of light parallel to the principal axis are falling on a concave lens. 
  • These rays, after refraction from the lens, are appearing to diverge from a point on the principal axis. 
  • This point on the principal axis is called the principal focus of the concave lens.

• If parallel rays pass from the opposite surface of the lens,  another principal focus on the opposite side is made. 
• Letter F is usually used to represent principal focus. 
  • However, a lens has two principal foci. 
  • They are represented by F1 and F2 . 
• The distance of the principal focus from the optical centre of a lens is called its focal length. 
• The letter f is used to represent the focal length.

Spherical Lens Image Formation: Illuminating Perspectives through Ray Diagrams:

• For drawing ray diagrams in lenses, alike of spherical mirrors, we consider any two of the following rays –
• (i) A ray of light from the object, parallel to the principal axis, after refraction from a convex lens, passes through the principal focus on the other side of the lens. 
  • In case of a concave lens, the ray appears to diverge from the principal focus located on the same side of the lens.

• (ii) A ray of light passing through a principal focus, after refraction from a convex lens, will emerge parallel to the principal axis. 
  • A ray of light appearing to meet at the principal focus of a concave lens, after refraction, will emerge parallel to the principal axis.

• (iii) A ray of light passing through the optical centre of a lens will emerge without any deviation. 
  • The ray diagrams for the image formation in a convex lens for a few positions  of  the  object.

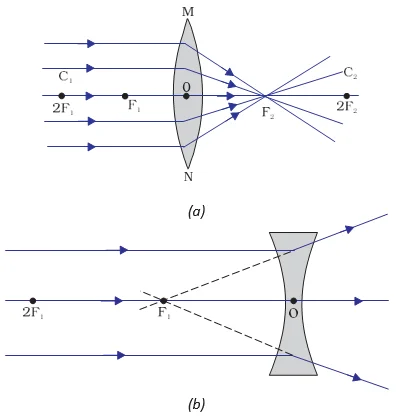
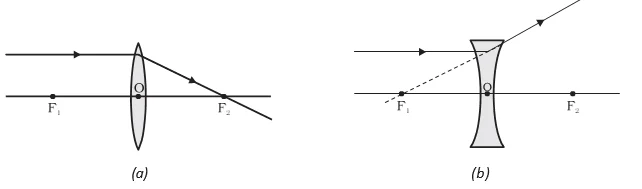
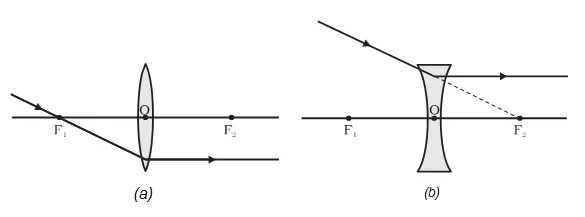
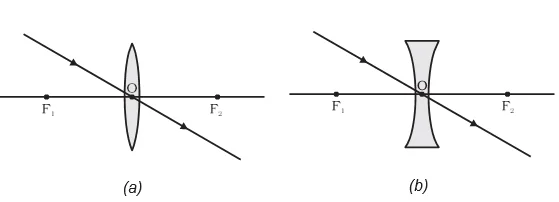
Spherical Lens Image Formation and Optical Variations:

• Lenses form images by refracting light. 
• The nature, position and relative size of the image formed by a convex and concave lens for various positions of the object is summarized in the table.

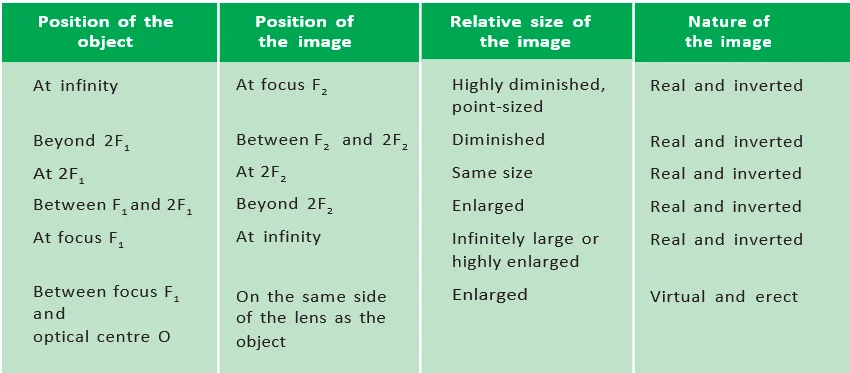
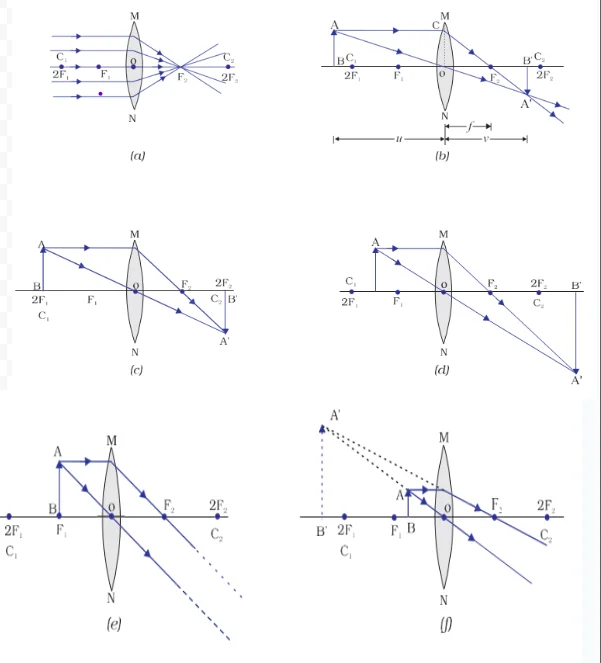
In conclusion it can be said that a concave lens will always give a virtual, erect and diminished image, irrespective of the position of the object.

Spherical Lens Sign Convention: Optical Measurements and Focal Insights 

• For lenses, the sign convention is similar to that used for mirrors.  
• All the rules for signs of distances are applied except that all measurements are taken from the optical centre of the lens. 
• According to the convention, the focal length of a convex lens is positive and that of a concave lens is negative.

Spherical Lens Formula: Understanding Relationships in Optics:

• This formula gives the relationship between object distance (u), image-distance (v) and the focal length (f). 
  • The lens formula is expressed as 1/v – 1/u = 1/f
• The lens formula given above is general and is valid in all situations for any spherical lens.

Spherical Lens Magnification: Optical Enlargement and Relationships

• The magnification produced by a lens, similar to that for spherical mirrors, is defined as the ratio of the height of the image and the height of the object. 
• Magnification is represented by the letter m. 
• If h is the height of the object and h′ is the height of the image given by a lens, then the magnification produced by the lens is given by,

• Magnification produced by a lens is also related to the object-distance u, and the image-distance v. 
  • This relationship is given by: Magnification (m) = h′/h = v/u

Spherical Lens Power Dynamics: Optical Convergence and Divergence

• The ability of a lens to converge or diverge light rays depends on its focal length. 
  • Example: A convex lens of short focal length bends the light rays through large angles, by focussing them closer to the optical centre. 
  • Similarly, concave lenses of very short focal length cause higher divergence than the one with longer focal length. 
• The degree of convergence or divergence of light rays achieved by a lens is expressed in terms of its power. 
• The power of a lens is defined as the reciprocal of its focal length. 
  • It is represented by the letter P. 
  • The power P of a lens of focal length f is given by: 

• The SI unit of power of a lens is ‘dioptre’. 
  • It is denoted by the letter D. 
• If ‘f’ is expressed in metres, then, the power is expressed in dioptres. 
• Thus, 1 dioptre is the power of a lens whose focal length is 1 metre. 1D = 1m-1. 
• The power of a convex lens is positive and that of a concave lens is negative. 
• Opticians prescribe corrective lenses indicating their powers.

DOWNLOAD PDF