Exploring the strategic significance of Mathematics as an optional subject in UPSC IFS Mains, with insights into its scoring potential, paper format, and trend analysis. Unlocking success with a comprehensive overview, including exam overview, success rates, and expert-recommended booklist for effective preparation

The UPSC IFS mains consist of a total of six papers with a total of 1400 marks. The IFS Mains examination includes two papers: one on English and one on General Knowledge. The remaining four papers (Paper I, Paper II, Paper III and Paper IV) cover optional subjects that candidates have chosen during the application form filling process. Since Paper I and Paper II have a maximum of 300 marks each, the remaining 800 marks depend on the optional subjects. It becomes crucial to choose the right optional subject and employ the right strategy so that candidates can score as much as possible. First, we will explore the importance and weightage of optionals, and then we will analyze Mathematics Optional subjects.
| Download IFS 2023 Mathematics Optional Paper-01 Download IFS 2023 Mathematics Optional Paper-02 |
In UPSC IFS mains examination candidates have to choose two optional subjects from the list specified in the notification unlike UPSC IAS mains exam in which candidate has to choose only one optional subject. In IFS exam optional subjects have very high scoring potential because after Paper I and Paper II which consist of 600 marks optional have 800 marks so here optional plays a decisive role in determining your selection as well as to achieve a good rank.

It is evident that in the entire selection process, the optional subject plays a crucial role in preparing for the UPSC IFS exam, as it accounts for almost 48% of the total marks. This substantial portion contributes significantly to the overall evaluation of the entire exam.
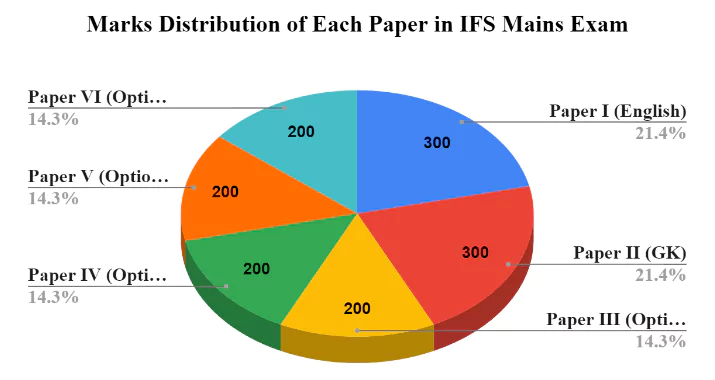
Upon further magnification, we can conclude that in the IFS mains examination, the Mathematics Optional section carries almost 58% of the total mains marks. Therefore, scoring well in the optional section, along with Paper I and Paper II, will result in higher overall marks in the exam.
In the UPSC IFS Mains exam, Mathematics optional subject consists of two papers, specifically Paper I and Paper II. Each of these papers carries a weightage of 200 marks, summing up to a total of 400 marks for this optional subject. Among the various optional subjects offered by UPSC in IFS, Mathematics is one of the 14 optional subjects available to candidates.
| Mathematics Optional | Syllabus of Mathematics Optional |
| Paper I of Mathematics Optional | Linear Algebra- Vector, space, linear dependence and independence, subspaces, bases, dimensions. Finite dimensional vector spaces. Matrices, Cayley-Hamiliton theorem, Eigenvalues and Eigenvectors, matrix of linear transformation, row and column reduction, Echelon form, equivalence, congruence and similarity, reduction to canonical form, rank, orthogonal, symmetrical, skew symmetrical, unitary, hermitian, skew-hermitian forms their Eigenvalues. Orthogonal and unitary reduction of quadratic and hermitian forms, positive definite quadratic forms.
Calculus– Real numbers, limits, continuity, differentiability, mean-value theorems, Taylor’s theorem with remainders, indeterminate forms, maxima and minima, asymptotes. Functions of several variables: continuity, differentiability, partial derivatives, maxima and minima, Lagrange’s method of multipliers, Jacobian. Riemann’s definition of definite integrals, indefinite integrals, infinite and improper integrals, beta and gamma functions. Double and triple integrals (evaluation techniques only). Areas, surface and volumes, centre of gravity. Analytic Geometry- Cartesian and polar coordinates in two and three dimensions, second degree equations in two and three dimensions, reduction to canonical forms, straight lines, shortest distance between two skew lines, plane, sphere, cone, cylinder, paraboloid, ellipsoid, hyperboloid of one and two sheets and their properties. Ordinary Differential Equations- Formulation of differential equations, order and degree, equations of first order and first degree, integrating factor, equations of first order but not of first degree, Clariaut’s equation, singular solution. Higher order linear equations, with constant coefficients, complementary function and particular integral, general solution, EulerCauchy equation. Second order linear equations with variable coefficients, determination of complete solution when one solution is known, method of variation of parameters. Dynamics, Statics and Hydrostatics- Degree of freedom and constraints, rectilinear motion, simple harmonic motion, motion in a plane, projectiles, constrained motion, work and energy, conservation of energy, motion under impulsive forces, Kepler’s laws, orbits under central forces, motion of varying mass, motion under resistance. Equilibrium of a system of particles, work and potential energy, friction, common catenary, principle of virtual work, stability of equilibrium, equilibrium of forces in three dimensions. 41 Pressure of heavy fluids, equilibrium of fluids under given system of forces Bernoulli’s equation, centre of pressure, thrust on curved surfaces, equilibrium of floating bodies, stability of equilibrium, metacentre, pressure of gases. Vector Analysis- Scalar and vector fields, triple, products, differentiation of vector function of a scalar variable, gradient, divergence and curl in cartesian, cylindrical and spherical coordinates and their physical interpretations. Higher order derivatives, vector identities and vector equations. Application to Geometry: Curves in space, curvature and torsion. Serret-Frenet’s formulae, Gauss and Stokes’ theorems, Green’s identities. |
| Paper II of Mathematics Optional | Algebra- Groups, subgroups, normal subgroups, homomorphism of groups, quotient groups, basic isomorphism theorems, Sylow’s group, permutation groups, Cayley theorem. Rings and ideals, principal ideal domains, unique factorization domains and Euclidean domains. Field extensions, finite fields.
Real Analysis- Real number system, ordered sets, bounds, ordered field, real number system as an ordered field with least upper bound property, Cauchy sequence, completeness, Continuity and uniform continuity of functions, properties of continuous functions on compact sets. Riemann integral, improper integrals, absolute and conditional convergence of series of real and complex terms, rearrangement of series. Uniform convergence, continuity, differentiability and integrability for sequences and series of functions. Differentiation of functions of several variables, change in the order of partial derivatives, implicit function theorem, maxima and minima. Multiple integrals. Complex Analysis- Analytic function, Cauchy-Riemann equations, Cauchy’s theorem, Cauchy’s integral formula, power series, Taylor’s series, Laurent’s Series, Singularities, Cauchy’s residue theorem, contour integration. Conformal mapping, bilinear transformations. Linear Programming- Linear programming problems, basic solution, basic feasible solution and optimal solution, graphical method and Simplex method of solutions. Duality. Transportation and assignment problems. Traveling salesman problems. Partial differential equations- Curves and surfaces in three dimensions, formulation of partial differential equations, solutions of equations of type dx/p=dy/q=dz/r; orthogonal trajectories, Pfaffian differential equations; partial differential equations of the first order, solution by Cauchy’s method of characteristics; Charpit’s method of solutions, linear partial differential equations of the second order with constant coefficients, equations of vibrating string, heat equation, laplace equation. Numerical Analysis and Computer programming: Numerical methods: Solution of algebraic and transcendental equations of one variable by bisection, Regula-Falsi and Newton-Raphson methods, solution of system of linear equations by Gaussian elimination and Gauss-Jordan (direct) methods, Gauss-Seidel(iterative) method. Newton’s (Forward and backward) and Lagrange’s method of interpolation. Numerical integration- Simpson’s one-third rule, trapezoidal rule, Gaussian quadrature formula. Numerical solution of ordinary differential equations: Euler and Runge Kutta Methods. Computer Programming- Storage of numbers in Computers, bits, bytes and words, binary system. arithmetic and logical operations on numbers. Bitwise operations. AND, OR , XOR, NOT, and shift/rotate operators. Octal and Hexadecimal Systems. Conversion to and Form decimal Systems. Representation of unsigned integers, signed integers and reals, double precision reals and long integers. 42 Algorithms and flow charts for solving numerical analysis problems. Developing simple programs in Basic for problems involving techniques covered in the numerical analysis. Mechanics and Fluid Dynamics- Generalised coordinates, constraints, holonomic and non-holonomic systems. D’Alembert’s principle and Lagrange’ equations, Hamilton equations, moment of intertia, motion of rigid bodies in two dimensions. Equation of continuity, Euler’s equation of motion for inviscid flow, stream-lines, path of a particle, potential flow, two-dimensional and axisymmetric motion, sources and sinks, vortex motion, flow past a cylinder and a sphere, method of images. NavierStokes equation for a viscous fluid. |
UPSC Mathematics Optional Question Papers from 2018 to 2022 are readily available for aspirants seeking to enhance their preparation. We provided access to the UPSC IFS Mathematics optional question papers in PDF format, an invaluable resource for your preparation.
| Year | Paper of Mathematics Optional |
| UPSC IFS Mathematics Optional Question Paper 2018 | Download Paper I |
| UPSC IFS Mathematics Optional Question Paper 2019 | Download Paper I |
| UPSC IFS Mathematics Optional Question Paper 2020 | Download Paper I |
| UPSC IFS Mathematics Optional Question Paper 2021 | Download Paper I |
| UPSC IFS Mathematics Optional Question Paper 2022 | Download Paper I |
Candidates appearing for the UPSC (Union Public Service Commission) IFS examination must make a thoughtful choice when selecting their optional subject, as it holds substantial weightage in the evaluation process. With a total of 800 marks allotted, the optional subject constitutes approximately 48% of the combined marks for both the written exam and the personality test.
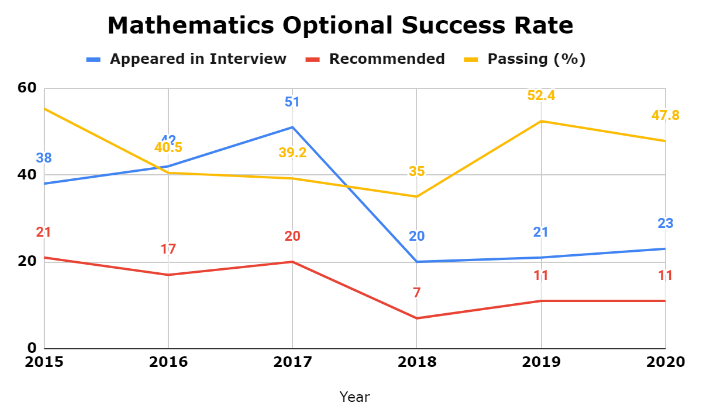
The table below offers a comprehensive overview of the success rate achieved by candidates who opted for Mathematics as their optional.
| Year | Number of Candidates appeared for Mathematics Optional | ||
|---|---|---|---|
| Appeared in Interview | Recommended | Passing (%) | |
| 2015 | 38 | 21 | 55.3 |
| 2016 | 42 | 17 | 40.5 |
| 2017 | 51 | 20 | 39.2 |
| 2018 | 20 | 7 | 35 |
| 2019 | 21 | 11 | 52.4 |
| 2020 | 23 | 11 | 47.8 |
By examining the past papers of the Mathematics Optional, we can identify a trend in the types of questions asked. There is also a noticeable shift in the themes of the questions. Understanding the UPSC IFS Mathematics Question Paper Trend Analysis is advantageous, as it allows candidates to streamline their preparation effectively and enhance their performance in this optional subject.
Please note that before selecting Mathematics as your optional subject, carefully weigh these disadvantages against the advantages and consider your own background, interests, and the time you can dedicate to preparation.
| Must Read | |
| NCERT Notes For UPSC | UPSC Daily Current Affairs |
| UPSC Blogs | UPSC Daily Editorials |
| Daily Current Affairs Quiz | Daily Main Answer Writing |
| UPSC Mains Previous Year Papers | UPSC Test Series 2024 |

<div class="new-fform">
</div>