Market Equilibrium: Demand, Supply, and Practical Insights

In this chapter, a combination of  consumer and firm  is used to analyze market equilibrium through demand and supply analysis. The price at which equilibrium occurs will be determined and the impacts of shifts in demand and supply on this equilibrium will be investigated. Additionally, Practical applications of demand and supply analysis will be examined.

Market Equilibrium, Excess Demand, Excess Supply: Balancing Act

• In a competitive market equilibrium, both buyers and sellers pursue self-interested goals. Consumers aim to maximise their preferences, while firms seek to maximise profits. Importantly, these objectives align in market equilibrium.
• Equilibrium: It occurs when all plans of all consumers and firms coincide, resulting in a market-clearing state.
  • This means that the quantity all firms want to sell equals the quantity all consumers want to buy, making market supply equal to market demand.
  • The price at which this market equilibrium is reached is the market equilibrium price, and the corresponding quantity bought and sold is the market equilibrium quantity.
  • Therefore, (p*, q*) is an equilibrium if,

qD(p*)= qS(p*)

where p* is the equilibrium price, and qD(p*) and qS(p*) represent market demand and market supply at price p*.

• Excess Supply: When market supply surpasses market demand at a price,.
• Excess Demand: If market demand exceeds market supply at a price.
• Therefore, an alternative definition of equilibrium in a perfectly competitive market is the absence of excess demand or excess supply.
• A Lack of Equilibrium: It is a condition where market equilibrium supply doesn’t equal market demand. Here there’s a tendency for the price to change.

• Analyzing Market Equilibrium: Market demand and supply curves will be used to examine how supply and demand interact to determine market equilibrium when the number of firms is fixed.
• Figure depicts a perfectly competitive market with a fixed number of firms.
• Supply Curve: The market supply curve (SS) shows firms’ desired supply at various prices,
• Demand Curve: While the demand curve (DD) represents consumers’ willingness to purchase at different prices. 
• Market Equilibrium: It occurs where these two curves intersect, signifying that market demand equals market supply.
• At any other point, there is either excess supply or excess demand.
• Excess Demand: If the current price is p1, market demand is q₁, but market supply is only q₁‘, resulting in excess demand equal to q₁‘q₁. 
  • This drives the price up because some consumers are willing to pay more.
  • As the price rises, quantity demanded decreases, and quantity supplied increases, gradually moving the market equilibrium at price p*.
•  Excess Supply: If the price is p₂, market supply (q₁) exceeds market demand (q₁‘), leading to excess supply of q_2′q₂. 
  • To sell their desired output, some firms lower their prices.
  • As the price falls, quantity demanded rises, and quantity supplied decreases until market equilibrium is reached at price p*, where market demand matches market supply, resulting in an equilibrium price p* and the equilibrium quantity is q*.

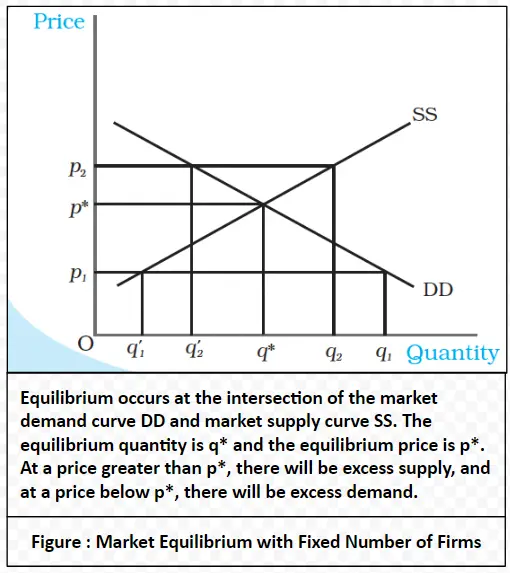
Let us consider the example of a market consisting of identical farms producing the same quality of wheat,

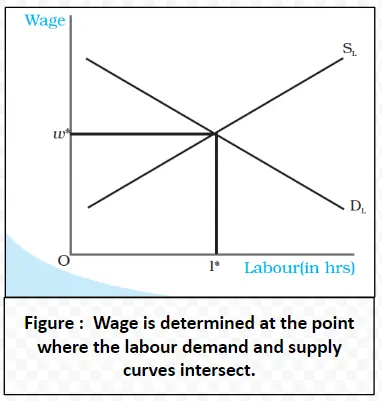
• In a perfectly competitive labor market, wage determination follows the principles of supply and demand analysis for Market Equilibrium. Unlike markets for goods, households supply labor, and firms demand it. 
• The wage rate: It is set where the labor supply and demand curves intersect.
• Assumptions and Market Conditions: To analyze the demand for labor by a single firm, we assume that
  • The Labor is the only variable input, 
  • The labor market is perfectly competitive and
  • The firm takes the wage rate as given. 
• Profit Maximization: The firm operates under profit maximization and adheres to the law of diminishing marginal product.
• Marginal Revenue Product of Labor (MRPL): When the firm hires labor until the additional cost (wage rate) of hiring one more unit of labor equals the additional benefit is called (MRPL).Thus, while hiring labor, the firm employs labor up to the point where

w = MRP_L

and MRP_L = MR × MP_L

• MRPL is calculated as the product of marginal revenue (MR) and the marginal product of labor MPL.
• Wage Rate and  (VMPL): 
  • As long as the Value of Marginal Product of Labor (VMPL) is greater than the wage rate, the firm will hire more labor, increasing profit.
  • Conversely, if VMPL is less than the wage rate, the firm can increase profit by reducing labor.
• Labour Demand Curve: Due to the law of diminishing marginal product, the firm’s labor demand curve slopes downward.
  • When the wage rate increases, VMPL must also rise, which can only happen if MPL increases.
  • However, because higher wages lead to diminishing returns, the firm employs less labor, resulting in a downward-sloping demand curve.
  • The market demand curve is derived by aggregating individual firm demand curves. Since each firm reduces labor demand as wages rise, the overall market demand curve also slopes downward.
• Labour Supply Curve: Turning to the supply side, households decide how much labor to provide at a given wage.
  • This involves a trade-off between leisure and income.
  • Single Labour Workforce Scenario: At low wages, people work more when wages rise, but at high wages, they work less. 
  • This leads to a backwards-bending individual labor supply curve.
  • Aggregate Individual Supply: In case of aggregate individual supply curves, we get an upward-sloping market supply curve for labor.
  • Despite some individuals working less at higher wages, many others are attracted to supply more labor.
• The Equilibrium Wage Rate: It is wage rate where the market supply curve intersects the market demand curve. This point signifies the balance between households’ desired labor supply and firms’ desired hiring, establishing market equilibrium.]

DOWNLOAD PDF